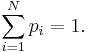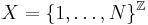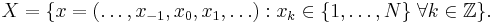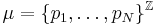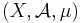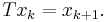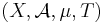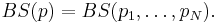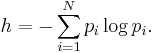Bernoulli scheme

In mathematics, the Bernoulli scheme or Bernoulli shift is a generalization of the Bernoulli process to more than two possible outcomes.[1][2] Bernoulli schemes are important in the study of dynamical systems, as most such systems (such as Axiom A systems) exhibit a repellor that is the product of the Cantor set and a smooth manifold, and the dynamics on the Cantor set are isomorphic to that of the Bernoulli shift.[3] This is essentially the Markov partition. The term shift is in reference to the shift operator, which may be used to study Bernoulli schemes. The Ornstein isomorphism theorem[4] shows that Bernoulli shifts are isomorphic when their entropy is equal. Finite stationary stochastic processes are isomorphic to the Bernoulli shift; in this sense, Bernoulli shifts are universal.

Contents

Definition

A Bernoulli scheme is a discrete-time stochastic process where each independent random variable may take on one of N distinct possible values, with the outcome i occurring with probability 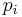p_i, with i = 1, ..., N, and

\sum_{i=1}^N p_i = 1.

The sample space is usually denoted as

X=\{1,\ldots,N \}^\mathbb{Z}

as a short-hand for

X=\{ x=(\ldots,x_{-1},x_0,x_1,\ldots)�: x_k \in \{1,\ldots,N\} \; \forall k \in \mathbb{Z} \}.

The associated measure is

\mu = \{p_1,\ldots,p_N\}^\mathbb{Z}

The σ-algebra 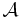\mathcal{A} on X is the product sigma algebra; that is, it is the (infinite) product of the σ-algebras of the finite set {1, ..., N}. Thus, the triplet

(X,\mathcal{A},\mu)

is a measure space. The Bernoulli scheme, as any stochastic process, may be viewed as a dynamical system by endowing it with the shift operator T where

Tx_k = x_{k%2B1}.

Since the outcomes are independent, the shift preserves the measure, and thus T is a measure-preserving transformation. The quadruplet

(X,\mathcal{A},\mu, T)

is a measure-preserving dynamical system, and is called a Bernoulli scheme or a Bernoulli shift. It is often denoted by

BS(p)=BS(p_1,\ldots,p_N).

The N = 2 Bernoulli scheme is called a Bernoulli process. The Bernoulli shift can be understood as a special case of the Markov shift, where all entries in the adjacency matrix are one, the corresponding graph thus being a clique.

Properties

The Bernoulli scheme is a stationary stochastic process; conversely, all finite stationary stochastic processes, including subshifts of finite type and finite Markov chains, are Bernoulli schemes; this is essentially the content of the Ornstein isomorphism theorem.

Ya. Sinai demonstrated that the Kolmogorov entropy of a Bernoulli scheme is given by

h = -\sum_{i=1}^N p_i \log p_i .

The isomorphism theorem for Bernoulli schemes, sometimes called the Ornstein isomorphism theorem, proven by Donald Ornstein in 1968, states that two Bernoulli schemes with the same entropy are isomorphic. Here isomorphic means that if X and Y are two sample spaces, then there exists a function between these two that is measurable and invertible, that commutes with the measures, and that commutes with the shift operators for almost all sequences in X and Y. A simplified proof of the isomorphism theorem was given by Michael S. Keane and M. Smorodinsky in 1979.

When N is a prime number, sequences in the sample space may be represented by p-adic numbers. If the probabilities are uniform, that is, each 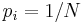p_i=1/N, then the distribution of sequences corresponds to a uniform measure on the space of numbers. As a result, the results from p-adic analysis may be applied.

See also

References

  1. ^ P. Shields, The theory of Bernoulli shifts , Univ. Chicago Press (1973)
  2. ^ Michael S. Keane, "Ergodic theory and subshifts of finite type", (1991), appearing as Chapter 2 in Ergodic Theory, Symbolic Dynamics and Hyperbolic Spaces, Tim Bedford, Michael Keane and Caroline Series, Eds. Oxford University Press, Oxford (1991). ISBN 0-19-853390-X
  3. ^ Pierre Gaspard, Chaos, scattering and statistical mechanics(1998), Cambridge University press
  4. ^ D.S. Ornstein (2001), "Ornstein isomorphism theorem", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=O/o120070